bezier

与贝塞尔曲线相关的实用函数。

函数

bezier(points: BezierPointsLike) → Callable[[float | ColVector], Point3D | Point3D_Array]

bezier(points: Sequence[Point3DLike_Array]) → Callable[[float | ColVector], Point3D_Array]

贝塞尔曲线的经典实现。

参数:

points – 一个形状为 \((d+1, 3)\) 的数组，包含 \(d+1\) 个控制点，定义了一条 \(d\) 次贝塞尔曲线。另外，为了向量化，points 也可以是一个形状为 \((d+1, M, 3)\) 的序列，包含 \(d+1\) 个数组，每个数组有 \(M\) 个控制点，这样可以定义 M 条贝塞尔曲线。

返回:

bezier_func – 描述贝塞尔曲线的函数。此函数的行为取决于 points 的形状。

• 如果 points 是一个表示单个贝塞尔曲线的 \((d+1, 3)\) 数组，那么 bezier_func 可以接收以下类型：

  • 一个 float t，在这种情况下，它会返回一个形状为 \((1, 3)\) 的 Point3D，表示贝塞尔曲线在 t 处的求值，或者

  • 一个形状为 \((n, 1)\) 的 ColVector，包含 \(n\) 个用于评估贝塞尔曲线的值，并返回一个形状为 \((n, 3)\) 的 Point3D_Array，其中包含在 \(n\) 个值处评估贝塞尔曲线所得到的点。

  警告

  如果将 \(t\) 值的向量传递给 bezier_func，它必须是形状为 \((n, 1)\) 的列向量/矩阵。不支持传递形状为 \((n,)\) 的一维数组，这会导致未定义行为。

• 如果 points 是一个描述 \(M\) 条贝塞尔曲线的 \((d+1, M, 3)\) 数组，那么 bezier_func 可以接收以下类型：

  • 一个 float t，在这种情况下，它会返回一个形状为 \((M, 3)\) 的 Point3D_Array，表示 \(M\) 条贝塞尔曲线在相同值 t 处的求值，或者

  • 一个形状为 \((M, 1)\) 的 ColVector，包含 \(M\) 个值，这样由 points 定义的第 \(i\) 条贝塞尔曲线会在 t 中对应的第 \(i\) 个值处进行评估，并再次返回一个形状为 \((M, 3)\) 的 Point3D_Array，其中包含这 \(M\) 个评估结果。

  警告

  与上一种情况不同，如果将 ColVector 传递给 bezier_func，它必须正好包含 \(M\) 个值，每个值对应由 points 定义的 \(M\) 条贝塞尔曲线中的每一条。任何形状不是 \((M, 1)\) 的数组都会导致未定义行为。

返回类型:

typing.Callable [[float | ColVector], Point3D | Point3D_Array]

bezier_remap(bezier_tuples, new_number_of_curves)

将 bezier_tuples 中的每条曲线细分为所需的部分，直到最终曲线数量达到期望值 new_number_of_curves。

参数:

• bezier_tuples (BezierPointsLike_Array) –

  一个由多个 \(d\) 次贝塞尔曲线组成的数组，用于重新映射。该数组的形状必须是 (current_number_of_curves, nppc, dim)，其中

  • current_number_of_curves 是数组 bezier_tuples 中当前的曲线数量，

  • nppc 是每条曲线的点数，使得它们的次数为 nppc-1，并且

  • dim 是点的维度，通常为 \(3\)。

• new_number_of_curves (int) – 输出将包含的曲线数量。这需要高于当前数量。

返回:

形状为 (new_number_of_curves, nppc, dim) 的新数组，包含重新映射后的新贝塞尔曲线。

返回类型:

BezierPoints_Array

get_quadratic_approximation_of_cubic(a0: Point3DLike, h0: Point3DLike, h1: Point3DLike, a1: Point3DLike) → QuadraticSpline

get_quadratic_approximation_of_cubic(a0: Point3DLike_Array, h0: Point3DLike_Array, h1: Point3DLike_Array, a1: Point3DLike_Array) → QuadraticBezierPath

如果 a0、h0、h1 和 a1 是一条三次贝塞尔曲线的控制点，则用两条二次贝塞尔曲线来近似该曲线，并返回一个包含 6 个点的数组，其中前 3 个点表示第一条二次曲线，后 3 个点表示第二条。

否则，如果 a0、h0、h1 和 a1 是表示 \(N\) 条三次贝塞尔曲线的 \(N\) 个点的数组，则返回一个包含 \(6N\) 个点的数组，其中每组 \(6\) 个连续点以类似上述方式近似 \(N\) 条曲线中的每一条。

注意

如果原始三次贝塞尔曲线所组成的三次样条是平滑的，则此算法将生成一个同样平滑的二次样条。

如果一条三次贝塞尔曲线由以下给出：

\[C(t) = (1-t)^3 A_0 + 3(1-t)^2 t H_0 + 3(1-t)t^2 H_1 + t^3 A_1\]

其中 \(A_0\)、\(H_0\)、\(H_1\) 和 \(A_1\) 是其控制点，则此算法应生成以下两条二次贝塞尔曲线：

\[\begin{split}Q_0(t) &= (1-t)^2 A_0 + 2(1-t)t M_0 + t^2 K \\ Q_1(t) &= (1-t)^2 K + 2(1-t)t M_1 + t^2 A_1\end{split}\]

其中 \(M_0\) 和 \(M_1\) 是两条曲线各自要找到的句柄，\(K\) 是第一条曲线的终点锚点和第二条曲线的起点锚点，同样需要找到。

为了求解 \(M_0\)、\(M_1\) 和 \(K\)，可以施加三个条件：

1. \(Q_0'(0) = \frac{1}{2}C'(0)\)。第一条二次曲线在 \(t = 0\) 处的导数应与原始三次曲线在 \(t = 0\) 处的导数成比例。由于三次曲线被分成两部分，因此需要将其除以二：点沿着曲线移动的速度应是原始速度的一半。这得出：

   \[\begin{split}Q_0'(0) &= \frac{1}{2}C'(0) \\ 2(M_0 - A_0) &= \frac{3}{2}(H_0 - A_0) \\ 2M_0 - 2A_0 &= \frac{3}{2}H_0 - \frac{3}{2}A_0 \\ 2M_0 &= \frac{3}{2}H_0 + \frac{1}{2}A_0 \\ M_0 &= \frac{1}{4}(3H_0 + A_0)\end{split}\]

2. \(Q_1'(1) = \frac{1}{2}C'(1)\)。第二条二次曲线在 \(t = 1\) 处的导数应是原始三次曲线在 \(t = 1\) 处导数的一半，原因同上。这得出：

   \[\begin{split}Q_1'(1) &= \frac{1}{2}C'(1) \\ 2(A_1 - M_1) &= \frac{3}{2}(A_1 - H_1) \\ 2A_1 - 2M_1 &= \frac{3}{2}A_1 - \frac{3}{2}H_1 \\ -2M_1 &= -\frac{1}{2}A_1 - \frac{3}{2}H_1 \\ M_1 &= \frac{1}{4}(3H_1 + A_1)\end{split}\]

3. \(Q_0'(1) = Q_1'(0)\)。两条二次曲线的导数在点 \(K\) 处应匹配，以使最终样条平滑。这得出：

   \[\begin{split}Q_0'(1) &= Q_1'(0) \\ 2(K - M_0) &= 2(M_1 - K) \\ 2K - 2M_0 &= 2M_1 - 2K \\ 4K &= 2M_0 + 2M_1 \\ K &= \frac{1}{2}(M_0 + M_1)\end{split}\]

这足以找到二次贝塞尔曲线的正确控制点。

参数:

• a0 – 单个三次贝塞尔曲线的起始锚点，或者是 \(N\) 条曲线的 \(N\) 个起始锚点数组。

• h0 – 单个三次贝塞尔曲线的第一个句柄，或者是 \(N\) 条曲线的 \(N\) 个第一个句柄数组。

• h1 – 单个三次贝塞尔曲线的第二个句柄，或者是 \(N\) 条曲线的 \(N\) 个第二个句柄数组。

• a1 – 单个三次贝塞尔曲线的结束锚点，或者是 \(N\) 条曲线的 \(N\) 个结束锚点数组。

返回:

一个数组，包含 6 个点用于近似原始三次曲线的两条二次贝塞尔曲线，或者 \(6N\) 个点用于近似 \(N\) 条三次曲线的 \(2N\) 条二次曲线。

返回类型:

结果

抛出:

ValueError – 如果 a0、h0、h1 和 a1 具有不同的维度，或者它们的维度数不是 1 或 2。

get_smooth_closed_cubic_bezier_handle_points(anchors)

get_smooth_cubic_bezier_handle_points() 的特例，当 anchors 形成闭合循环时。

注意

必须解方程组才能得到每条贝塞尔曲线的第一个句柄（称为 \(H_1\)）。然后 \(H_2\)（第二个句柄）可以单独获得。

另请参阅

这些方程来源于：

• 控制点实现连续曲率的条件。(2016). Jaco Stuifbergen。

通常，如果有 \(N+1\) 个锚点，就会有 \(N\) 条贝塞尔曲线，因此需要找到 \(N\) 对句柄。我们必须为第一个句柄（以 \(N = 5\) 为例）求解以下方程组：

\[\begin{split}\begin{pmatrix} 4 & 1 & 0 & 0 & 1 \\ 1 & 4 & 1 & 0 & 0 \\ 0 & 1 & 4 & 1 & 0 \\ 0 & 0 & 1 & 4 & 1 \\ 1 & 0 & 0 & 1 & 4 \end{pmatrix} \begin{pmatrix} H_{1,0} \\ H_{1,1} \\ H_{1,2} \\ H_{1,3} \\ H_{1,4} \end{pmatrix} = \begin{pmatrix} 4A_0 + 2A_1 \\ 4A_1 + 2A_2 \\ 4A_2 + 2A_3 \\ 4A_3 + 2A_4 \\ 4A_4 + 2A_5 \end{pmatrix}\end{split}\]

这将被表示为 \(RH_1 = D\)。

\(R\) 几乎是一个三对角矩阵，所以我们可以使用托马斯算法。

另请参阅

三对角矩阵算法。维基百科。

然而，\(R\) 在对角有 1。解决这个问题的方法是下面链接中提出的第一个分解，其中 \(\alpha = 1\)

另请参阅

三对角矩阵算法 # 变体。维基百科。

\[\begin{split}R = \begin{pmatrix} 4 & 1 & 0 & 0 & 1 \\ 1 & 4 & 1 & 0 & 0 \\ 0 & 1 & 4 & 1 & 0 \\ 0 & 0 & 1 & 4 & 1 \\ 1 & 0 & 0 & 1 & 4 \end{pmatrix} &= \begin{pmatrix} 3 & 1 & 0 & 0 & 0 \\ 1 & 4 & 1 & 0 & 0 \\ 0 & 1 & 4 & 1 & 0 \\ 0 & 0 & 1 & 4 & 1 \\ 0 & 0 & 0 & 1 & 3 \end{pmatrix} + \begin{pmatrix} 1 & 0 & 0 & 0 & 1 \\ 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 \\ 1 & 0 & 0 & 0 & 1 \end{pmatrix} \\ & \\ &= \begin{pmatrix} 3 & 1 & 0 & 0 & 0 \\ 1 & 4 & 1 & 0 & 0 \\ 0 & 1 & 4 & 1 & 0 \\ 0 & 0 & 1 & 4 & 1 \\ 0 & 0 & 0 & 1 & 3 \end{pmatrix} + \begin{pmatrix} 1 \\ 0 \\ 0 \\ 0 \\ 1 \end{pmatrix} \begin{pmatrix} 1 & 0 & 0 & 0 & 1 \end{pmatrix} \\ & \\ &= T + uv^t\end{split}\]

我们将 \(R = T + uv^t\) 分解，其中 \(T\) 是一个三对角矩阵，\(u, v\) 是 \(N\) 维向量，满足 \(u_0 = u_{N-1} = v_0 = v_{N-1} = 1\)，并且 \(u_i = v_i = 0, \forall i \in \{1, ..., N-2\}\)。

因此

\[\begin{split}RH_1 &= D \\ \Rightarrow (T + uv^t)H_1 &= D\end{split}\]

如果我们找到一个向量 \(q\) 使得 \(Tq = u\)

\[\begin{split}\Rightarrow (T + Tqv^t)H_1 &= D \\ \Rightarrow T(I + qv^t)H_1 &= D \\ \Rightarrow H_1 &= (I + qv^t)^{-1} T^{-1} D\end{split}\]

根据谢尔曼-莫里森公式

另请参阅

谢尔曼-莫里森公式。维基百科。

\[(I + qv^t)^{-1} = I - \frac{1}{1 + v^tq} qv^t\]

如果我们找到 \(Y = T^{-1} D\)，换句话说，如果我们求解 \(TY = D\) 中的 \(Y\)

\[\begin{split}H_1 &= (I + qv^t)^{-1} T^{-1} D \\ &= (I + qv^t)^{-1} Y \\ &= (I - \frac{1}{1 + v^tq} qv^t) Y \\ &= Y - \frac{1}{1 + v^tq} qv^tY\end{split}\]

因此，我们必须在 \(Tq = u\) 和 \(TY = D\) 中求解 \(q\) 和 \(Y\)。由于 \(T\) 现在是三对角矩阵，我们将使用托马斯算法。

定义

• \(a = [a_0, \ a_1, \ ..., \ a_{N-2}]\) 作为 \(T\) 的下对角线，包含 \(N-1\) 个元素，使得 \(a_0 = a_1 = ... = a_{N-2} = 1\)，因此该对角线填充为 1；

• \(b = [b_0, \ b_1, \ ..., \ b_{N-2}, \ b_{N-1}]\) 作为 \(T\) 的主对角线，包含 \(N\) 个元素，使得 \(b_0 = b_{N-1} = 3\)，且 \(b_1 = b_2 = ... = b_{N-2} = 4\)；

• \(c = [c_0, \ c_1, \ ..., \ c_{N-2}]\) 作为 \(T\) 的上对角线，包含 \(N-1\) 个元素，使得 \(c_0 = c_1 = ... = c_{N-2} = 1\)：该对角线也填充为 1。

如果根据托马斯算法，我们定义

\[\begin{split}c'_0 &= \frac{c_0}{b_0} & \\ c'_i &= \frac{c_i}{b_i - a_{i-1} c'_{i-1}}, & \quad \forall i \in \{1, ..., N-2\} \\ & & \\ u'_0 &= \frac{u_0}{b_0} & \\ u'_i &= \frac{u_i - a_{i-1} u'_{i-1}}{b_i - a_{i-1} c'_{i-1}}, & \quad \forall i \in \{1, ..., N-1\} \\ & & \\ D'_0 &= \frac{1}{b_0} D_0 & \\ D'_i &= \frac{1}{b_i - a_{i-1} c'_{i-1}} (D_i - a_{i-1} D'_{i-1}), & \quad \forall i \in \{1, ..., N-1\}\end{split}\]

则

\[\begin{split}c'_0 &= \frac{1}{3} & \\ c'_i &= \frac{1}{4 - c'_{i-1}}, & \quad \forall i \in \{1, ..., N-2\} \\ & & \\ u'_0 &= \frac{1}{3} & \\ u'_i &= \frac{-u'_{i-1}}{4 - c'_{i-1}} = -c'_i u'_{i-1}, & \quad \forall i \in \{1, ..., N-2\} \\ u'_{N-1} &= \frac{1 - u'_{N-2}}{3 - c'_{N-2}} & \\ & & \\ D'_0 &= \frac{1}{3} (4A_0 + 2A_1) & \\ D'_i &= \frac{1}{4 - c'_{i-1}} (4A_i + 2A_{i+1} - D'_{i-1}) & \\ &= c_i (4A_i + 2A_{i+1} - D'_{i-1}), & \quad \forall i \in \{1, ..., N-2\} \\ D'_{N-1} &= \frac{1}{3 - c'_{N-2}} (4A_{N-1} + 2A_N - D'_{N-2}) &\end{split}\]

最后，我们可以进行回代以找到 \(q\) 和 \(Y\)

\[\begin{split}q_{N-1} &= u'_{N-1} & \\ q_i &= u'_{i} - c'_i q_{i+1}, & \quad \forall i \in \{0, ..., N-2\} \\ & & \\ Y_{N-1} &= D'_{N-1} & \\ Y_i &= D'_i - c'_i Y_{i+1}, & \quad \forall i \in \{0, ..., N-2\}\end{split}\]

有了这些值，我们最终可以计算 \(H_1 = Y - \frac{1}{1 + v^tq} qv^tY\)。鉴于 \(v_0 = v_{N-1} = 1\)，且 \(v_1 = v_2 = ... = v_{N-2} = 0\)，它与 \(q\) 和 \(Y\) 的点积分别是 \(v^tq = q_0 + q_{N-1}\) 和 \(v^tY = Y_0 + Y_{N-1}\)。因此

\[H_1 = Y - \frac{1}{1 + q_0 + q_{N-1}} q(Y_0 + Y_{N-1})\]

一旦我们有了 \(H_1\)，我们可以通过以下方式获得 \(H_2\)（第二个句柄的数组）：

\[\begin{split}H_{2, i} &= 2A_{i+1} - H_{1, i+1}, & \quad \forall i \in \{0, ..., N-2\} \\ H_{2, N-1} &= 2A_0 - H_{1, 0} &\end{split}\]

因为矩阵 \(R\) 总是遵循相同的模式（\(T, u, v\) 也一样），我们可以为 \(c'\) 和 \(u'\) 定义一个备忘列表，以避免重复计算。然而，我们不能对 \(D\) 和 \(Y\) 进行备忘，因为它们总是不同的矩阵。我们也不能为 \(q\) 创建备忘录，但我们可以更快地计算它，因为 \(u'\) 可以被备忘。

参数:

anchors (Point3DLike_Array) – 闭合三次样条的锚点。

返回:

包含两个数组的元组：一个包含闭合三次样条中每条曲线的第一个句柄，另一个包含第二个句柄。

返回类型:

tuple [Point3D_Array, Point3D_Array]

get_smooth_cubic_bezier_handle_points(anchors)

给定一个三次样条的锚点数组（由连接的三次贝塞尔曲线组成的数组），计算每条曲线的第一个和第二个句柄，使生成的样条是平滑的。

参数:

anchors (Point3DLike_Array) – 三次样条的锚点。

返回:

包含两个数组的元组：一个包含三次样条中每条曲线的第一个句柄，另一个包含第二个句柄。

返回类型:

tuple [Point3D_Array, Point3D_Array]

get_smooth_open_cubic_bezier_handle_points(anchors)

get_smooth_cubic_bezier_handle_points() 的特例，当 anchors 不形成闭合循环时。

注意

必须解方程组才能得到每条贝塞尔曲线的第一个句柄（称为 \(H_1\)）。然后 \(H_2\)（第二个句柄）可以单独获得。

另请参阅

这些方程来源于：

• 通过给定点的平滑贝塞尔样条。(2012). Particle in Cell Consulting LLC。

• 控制点实现连续曲率的条件。(2016). Jaco Stuifbergen。

警告

第一个网页中的方程存在一些笔误，已在评论中纠正。

通常，如果有 \(N+1\) 个锚点，就会有 \(N\) 条贝塞尔曲线，因此需要找到 \(N\) 对句柄。我们必须为第一个句柄（以 \(N = 5\) 为例）求解以下方程组：

\[\begin{split}\begin{pmatrix} 2 & 1 & 0 & 0 & 0 \\ 1 & 4 & 1 & 0 & 0 \\ 0 & 1 & 4 & 1 & 0 \\ 0 & 0 & 1 & 4 & 1 \\ 0 & 0 & 0 & 2 & 7 \end{pmatrix} \begin{pmatrix} H_{1,0} \\ H_{1,1} \\ H_{1,2} \\ H_{1,3} \\ H_{1,4} \end{pmatrix} = \begin{pmatrix} A_0 + 2A_1 \\ 4A_1 + 2A_2 \\ 4A_2 + 2A_3 \\ 4A_3 + 2A_4 \\ 8A_4 + A_5 \end{pmatrix}\end{split}\]

这将被表示为 \(TH_1 = D\)。\(T\) 是一个三对角矩阵，因此该系统可以在 \(O(N)\) 操作中求解。这里我们将使用托马斯算法或三对角矩阵算法。

另请参阅

三对角矩阵算法。维基百科。

定义

• \(a = [a_0, \ a_1, \ ..., \ a_{N-2}]\) 作为 \(T\) 的下对角线，包含 \(N-1\) 个元素，使得 \(a_0 = a_1 = ... = a_{N-3} = 1\)，且 \(a_{N-2} = 2\)；

• \(b = [b_0, \ b_1, \ ..., \ b_{N-2}, \ b_{N-1}]\) 作为 \(T\) 的主对角线，包含 \(N\) 个元素，使得 \(b_0 = 2\)，\(b_1 = b_2 = ... = b_{N-2} = 4\)，且 \(b_{N-1} = 7\)；

• \(c = [c_0, \ c_1, \ ..., \ c_{N-2}]\) 作为 \(T\) 的上对角线，包含 \({N-1}\) 个元素，使得 \(c_0 = c_1 = ... = c_{N-2} = 1\)：该对角线填充为 1。

如果根据托马斯算法，我们定义

\[\begin{split}c'_0 &= \frac{c_0}{b_0} & \\ c'_i &= \frac{c_i}{b_i - a_{i-1} c'_{i-1}}, & \quad \forall i \in \{1, ..., N-2\} \\ & & \\ D'_0 &= \frac{1}{b_0} D_0 & \\ D'_i &= \frac{1}{b_i - a_{i-1} c'{i-1}} (D_i - a_{i-1} D'_{i-1}), & \quad \forall i \in \{1, ..., N-1\}\end{split}\]

则

\[\begin{split}c'_0 &= 0.5 & \\ c'_i &= \frac{1}{4 - c'_{i-1}}, & \quad \forall i \in \{1, ..., N-2\} \\ & & \\ D'_0 &= 0.5A_0 + A_1 & \\ D'_i &= \frac{1}{4 - c'_{i-1}} (4A_i + 2A_{i+1} - D'_{i-1}) & \\ &= c_i (4A_i + 2A_{i+1} - D'_{i-1}), & \quad \forall i \in \{1, ..., N-2\} \\ D'_{N-1} &= \frac{1}{7 - 2c'_{N-2}} (8A_{N-1} + A_N - 2D'_{N-2}) &\end{split}\]

最后，我们可以进行回代以找到 \(H_1\)

\[\begin{split}H_{1, N-1} &= D'_{N-1} & \\ H_{1, i} &= D'_i - c'_i H_{1, i+1}, & \quad \forall i \in \{0, ..., N-2\}\end{split}\]

一旦我们有了 \(H_1\)，我们可以通过以下方式获得 \(H_2\)（第二个句柄的数组）：

\[\begin{split}H_{2, i} &= 2A_{i+1} - H_{1, i+1}, & \quad \forall i \in \{0, ..., N-2\} \\ H_{2, N-1} &= 0.5A_N + 0.5H_{1, N-1} &\end{split}\]

由于矩阵 \(T\) 总是遵循相同的模式，我们可以为 \(c'\) 定义一个备忘列表，以避免重复计算。然而，我们不能对 \(D\) 做同样的操作，因为它总是不同的矩阵。

参数:

anchors (Point3DLike_Array) – 开放三次样条的锚点。

返回:

包含两个数组的元组：一个包含开放三次样条中每条曲线的第一个句柄，另一个包含第二个句柄。

返回类型:

tuple [Point3D_Array, Point3D_Array]

integer_interpolate(start, end, alpha)

这是 interpolate 的一个变体，它返回一个整数和余数

参数:

• start (float) – 范围的起始值

• end (float) – 范围的结束值

• alpha (float) – 一个介于 0 和 1 之间的浮点数。

返回:

这会返回一个介于 start 和 end（包括两端）之间的整数，表示它们之间适当的插值，以及一个“余数”，表示返回整数与列表中下一个整数之间的新比例。

返回类型:

tuple[int, float]

示例

>>> integer, residue = integer_interpolate(start=0, end=10, alpha=0.46)
>>> np.allclose((integer, residue), (4, 0.6))
True

interpolate(start: float, end: float, alpha: float) → float

interpolate(start: float, end: float, alpha: ColVector) → ColVector

interpolate(start: Point3D, end: Point3D, alpha: float) → Point3D

interpolate(start: Point3D, end: Point3D, alpha: ColVector) → Point3D_Array

在两个值 start 和 end 之间进行线性插值。

参数:

• start – 范围的起始值。

• end – 范围的结束值。

• alpha – 一个介于 0 和 1 之间的浮点数，或者一个包含 \(n\) 个介于 0 和 1 之间浮点数的 \((n, 1)\) 列向量，用于向量化插值。

返回:

线性插值的结果。

• 如果 start 和 end 的类型是 float，并且

  • alpha 也是一个 float，则返回值只是另一个 float。

  • alpha 是一个 ColVector，则返回值是另一个 ColVector。

• 如果 start 和 end 的类型是 Point3D，并且

  • alpha 是一个 float，则返回值是另一个 Point3D。

  • alpha 是一个 ColVector，则返回值是 Point3D_Array。

返回类型:

float | ColVector | Point3D | Point3D_Array

inverse_interpolate(start: float, end: float, value: float) → float

inverse_interpolate(start: float, end: float, value: Point3D) → Point3D

inverse_interpolate(start: Point3D, end: Point3D, value: Point3D) → Point3D

执行逆插值，以确定在给定起始值和结束值或点的情况下，产生指定 value 的 alpha 值。

参数:

• start – 插值的起始值或点。

• end – 插值的结束值或点。

• value – 应确定其 alpha 值的数值或点。

返回:

• 产生给定输入的 alpha 值

• 在 start 和 end 之间进行插值时。

示例

>>> inverse_interpolate(start=2, end=6, value=4)
np.float64(0.5)

>>> start = np.array([1, 2, 1])
>>> end = np.array([7, 8, 11])
>>> value = np.array([4, 5, 5])
>>> inverse_interpolate(start, end, value)
array([0.5, 0.5, 0.4])

is_closed(points)

如果 points 给出的样条是闭合的，则返回 True，通过检查其第一个和最后一个点是否彼此接近，否则返回 False。

注意

此函数重新实现了 np.allclose()，因为仅对 2 个点重复调用 np.allclose() 效率低下。

参数:

points (Point3D_Array) – 定义样条的点数组。

返回:

数组的第一个和最后一个点是否足够接近以被视为相同，从而将定义的样条视为闭合。

返回类型:

bool

示例

>>> import numpy as np
>>> from manim import is_closed
>>> is_closed(
...     np.array(
...         [
...             [0, 0, 0],
...             [1, 2, 3],
...             [3, 2, 1],
...             [0, 0, 0],
...         ]
...     )
... )
True
>>> is_closed(
...     np.array(
...         [
...             [0, 0, 0],
...             [1, 2, 3],
...             [3, 2, 1],
...             [1e-10, 1e-10, 1e-10],
...         ]
...     )
... )
True
>>> is_closed(
...     np.array(
...         [
...             [0, 0, 0],
...             [1, 2, 3],
...             [3, 2, 1],
...             [1e-2, 1e-2, 1e-2],
...         ]
...     )
... )
False

match_interpolate(new_start: float, new_end: float, old_start: float, old_end: float, old_value: float) → float

match_interpolate(new_start: float, new_end: float, old_start: float, old_end: float, old_value: Point3D) → Point3D

将值从旧范围插值到新范围。

参数:

• new_start – 新范围的起始值。

• new_end – 新范围的结束值。

• old_start – 旧范围的起始值。

• old_end – 旧范围的结束值。

• old_value – 旧范围内的值，需要其在新范围中对应的（具有相同 alpha 值的）值。

返回类型:

新范围内的插值结果。

示例

>>> match_interpolate(0, 100, 10, 20, 15)
np.float64(50.0)

mid(start: float, end: float) → float

mid(start: Point3D, end: Point3D) → Point3D

返回两个值之间的中点。

参数:

• start – 第一个值

• end – 第二个值

返回类型:

两个值之间的中点

partial_bezier_points(points, a, b)

给定一个定义贝塞尔曲线的点数组，以及两个数 \(a, b\)，使得 \(0 \le a < b \le 1\)，返回一个相同大小的数组，该数组描述了原始贝塞尔曲线在区间 \([a, b]\) 上的部分。

partial_bezier_points() 在概念上等同于调用两次 split_bezier() 并丢弃未使用的贝塞尔曲线，但这种方法更高效，并且不会浪费计算。

另请参阅

有关如何分割贝塞尔曲线的解释，请参见 split_bezier()。

注意

要找到贝塞尔曲线在 \(t\) 介于 \(a\) 和 \(b\) 之间的部分

1. 在 \(t = a\) 处分割曲线并提取其第二个子曲线。

2. 我们不能在新子曲线上在 \(t = b\) 处进行评估，因为其 \(t\) 值的范围不同。要找到正确的值，我们需要通过首先减去 \(a\) 将区间 \([a, 1]\) 转换为 \([0, 1-a]\)，然后除以 \(1-a\)，将其转换为 \([0, 1]\)。因此，我们的新值必须是 \(t = \frac{b - a}{1 - a}\)。定义 \(u = \frac{b - a}{1 - a}\)。

3. 在 \(t = u\) 处分割子曲线并提取其第一个子曲线。

最终部分是点的线性组合，因此该过程可以总结为关于 \(a\) 和 \(b\) 的某个矩阵的线性变换。该矩阵对于在 Manim 中常用的小于等于 3 次的贝塞尔曲线明确给出。对于更高次，使用前面描述的算法。

对于二次贝塞尔曲线的情况

• 步骤 1

\[\begin{split}H'_1 = \begin{pmatrix} (1-a)^2 & 2(1-a)a & a^2 \\ 0 & (1-a) & a \\ 0 & 0 & 1 \end{pmatrix} \begin{pmatrix} p_0 \\ p_1 \\ p_2 \end{pmatrix}\end{split}\]

• 步骤 2

\[\begin{split}H''_0 &= \begin{pmatrix} 1 & 0 & 0 \\ (1-u) & u & 0\\ (1-u)^2 & 2(1-u)u & u^2 \end{pmatrix} H'_1 \\ & \\ &= \begin{pmatrix} 1 & 0 & 0 \\ (1-u) & u & 0\\ (1-u)^2 & 2(1-u)u & u^2 \end{pmatrix} \begin{pmatrix} (1-a)^2 & 2(1-a)a & a^2 \\ 0 & (1-a) & a \\ 0 & 0 & 1 \end{pmatrix} \begin{pmatrix} p_0 \\ p_1 \\ p_2 \end{pmatrix} \\ & \\ &= \begin{pmatrix} (1-a)^2 & 2(1-a)a & a^2 \\ (1-a)(1-b) & a(1-b) + (1-a)b & ab \\ (1-b)^2 & 2(1-b)b & b^2 \end{pmatrix} \begin{pmatrix} p_0 \\ p_1 \\ p_2 \end{pmatrix}\end{split}\]

由此可以定义一个 \((3, 3)\) 矩阵 \(P_2\)，当将其应用于点数组时，将返回所需的二次贝塞尔曲线部分

\[\begin{split}P_2 = \begin{pmatrix} (1-a)^2 & 2(1-a)a & a^2 \\ (1-a)(1-b) & a(1-b) + (1-a)b & ab \\ (1-b)^2 & 2(1-b)b & b^2 \end{pmatrix}\end{split}\]

类似地，对于三次贝塞尔曲线的情况，可以定义以下 \((4, 4)\) 矩阵 \(P_3\)

\[\begin{split}P_3 = \begin{pmatrix} (1-a)^3 & 3(1-a)^2a & 3(1-a)a^2 & a^3 \\ (1-a)^2(1-b) & 2(1-a)a(1-b) + (1-a)^2b & a^2(1-b) + 2(1-a)ab & a^2b \\ (1-a)(1-b)^2 & a(1-b)^2 + 2(1-a)(1-b)b & 2a(1-b)b + (1-a)b^2 & ab^2 \\ (1-b)^3 & 3(1-b)^2b & 3(1-b)b^2 & b^3 \end{pmatrix}\end{split}\]

参数:

• points (BezierPointsLike) – 定义贝塞尔曲线的点集。

• a (float) – 所需部分贝塞尔曲线的下限。

• b (float) – 所需部分贝塞尔曲线的上限。

返回:

包含定义部分贝塞尔曲线的控制点的数组。

返回类型:

BezierPoints

point_lies_on_bezier(point, control_points, round_to=1e-06)

检查给定点是否位于给定控制点的贝塞尔曲线上。

这是通过将该点作为常数项求解贝塞尔多项式来完成的；如果存在任何实根，则该点位于贝塞尔曲线上。

参数:

• point (Point3DLike) – 要检查点的笛卡尔坐标。

• control_points (BezierPointsLike) – 贝塞尔曲线的有序控制点的笛卡尔坐标，该点可能位于或不位于该曲线上。

• round_to (float) – 一个浮点数，所有值（例如点坐标）的小数位数将四舍五入到该浮点数指定的小数位数。

返回:

点是否位于曲线上。

返回类型:

bool

proportions_along_bezier_curve_for_point(point, control_points, round_to=1e-06)

根据给定点的贝塞尔曲线控制点，获取该点沿贝塞尔曲线的比例。

贝塞尔多项式是使用给定点的坐标以及贝塞尔曲线的控制点构建的。在求解每个维度的多项式时，如果每个维度都有共同的根，则这些根给出该点沿曲线的比例。如果没有实根，则该点不在曲线上。

参数:

• point (Point3DLike) – 应获取其参数的点的笛卡尔坐标。

• control_points (BezierPointsLike) – 贝塞尔曲线的有序控制点的笛卡尔坐标，该点可能位于或不位于该曲线上。

• round_to (float) – 一个浮点数，所有值（例如点坐标）的小数位数将四舍五入到该浮点数指定的小数位数。

返回:

包含贝塞尔曲线上给定点的可能参数（沿贝塞尔曲线的比例）的列表。这通常只包含一个或零个元素，但如果该点位于（例如）闭合循环的起点/终点，则可能返回一个包含多个值的列表，对应于循环的起点和终点等。

返回类型:

np.ndarray[float]

抛出:

ValueError – 当 point 和控制点具有不同形状时。

split_bezier(points, t)

将贝塞尔曲线在参数 t 处分割成两条曲线。

注意

另请参阅

贝塞尔曲线入门 #10：分割曲线。Pomax。

以三次贝塞尔曲线为例，令 \(p_0, p_1, p_2, p_3\) 为曲线 \(C_0 = [p_0, \ p_1, \ p_2, \ p_3]\) 所需的点。

定义 3 条线性贝塞尔曲线 \(L_0, L_1, L_2\)，作为 \(p_0, p_1, p_2, p_3\) 的插值

\[\begin{split}L_0(t) &= p_0 + t(p_1 - p_0) \\ L_1(t) &= p_1 + t(p_2 - p_1) \\ L_2(t) &= p_2 + t(p_3 - p_2)\end{split}\]

定义 2 条二次贝塞尔曲线 \(Q_0, Q_1\)，作为 \(L_0, L_1, L_2\) 的插值

\[\begin{split}Q_0(t) &= L_0(t) + t(L_1(t) - L_0(t)) \\ Q_1(t) &= L_1(t) + t(L_2(t) - L_1(t))\end{split}\]

那么 \(C_0\) 是 \(Q_0\) 和 \(Q_1\) 的以下插值

\[C_0(t) = Q_0(t) + t(Q_1(t) - Q_0(t))\]

在值 \(t=t'\) 处计算 \(C_0\) 会将 \(C_0\) 分割成两条三次贝塞尔曲线 \(H_0\) 和 \(H_1\)，由我们之前计算的某些点定义

\[\begin{split}H_0 &= [p_0, &\ L_0(t'), &\ Q_0(t'), &\ C_0(t') &] \\ H_1 &= [p_0(t'), &\ Q_1(t'), &\ L_2(t'), &\ p_3 &]\end{split}\]

由于所得曲线是通过 points 的线性组合获得的，因此一切都可以编码成矩阵以提高效率，这适用于三次及以下的贝塞尔曲线。

另请参阅

贝塞尔曲线入门 #11：使用矩阵分割曲线。Pomax。

对于二次贝塞尔曲线的更简单情况

\[\begin{split}H_0 &= \begin{pmatrix} p_0 \\ (1-t) p_0 + t p_1 \\ (1-t)^2 p_0 + 2(1-t)t p_1 + t^2 p_2 \\ \end{pmatrix} &= \begin{pmatrix} 1 & 0 & 0 \\ (1-t) & t & 0\\ (1-t)^2 & 2(1-t)t & t^2 \end{pmatrix} \begin{pmatrix} p_0 \\ p_1 \\ p_2 \end{pmatrix} \\ & \\ H_1 &= \begin{pmatrix} (1-t)^2 p_0 + 2(1-t)t p_1 + t^2 p_2 \\ (1-t) p_1 + t p_2 \\ p_2 \end{pmatrix} &= \begin{pmatrix} (1-t)^2 & 2(1-t)t & t^2 \\ 0 & (1-t) & t \\ 0 & 0 & 1 \end{pmatrix} \begin{pmatrix} p_0 \\ p_1 \\ p_2 \end{pmatrix}\end{split}\]

从中可以定义一个 \((6, 3)\) 分割矩阵 \(S_2\)，它可以乘以 points 数组以计算返回值

\[\begin{split}S_2 &= \begin{pmatrix} 1 & 0 & 0 \\ (1-t) & t & 0 \\ (1-t)^2 & 2(1-t)t & t^2 \\ (1-t)^2 & 2(1-t)t & t^2 \\ 0 & (1-t) & t \\ 0 & 0 & 1 \end{pmatrix} \\ & \\ S_2 P &= \begin{pmatrix} 1 & 0 & 0 \\ (1-t) & t & 0 \\ (1-t)^2 & 2(1-t)t & t^2 \\ (1-t)^2 & 2(1-t)t & t^2 \\ 0 & (1-t) & t \\ 0 & 0 & 1 \end{pmatrix} \begin{pmatrix} p_0 \\ p_1 \\ p_2 \end{pmatrix} = \begin{pmatrix} \vert \\ H_0 \\ \vert \\ \vert \\ H_1 \\ \vert \end{pmatrix}\end{split}\]

对于前面三次贝塞尔曲线的例子

\[\begin{split}H_0 &= \begin{pmatrix} p_0 \\ (1-t) p_0 + t p_1 \\ (1-t)^2 p_0 + 2(1-t)t p_1 + t^2 p_2 \\ (1-t)^3 p_0 + 3(1-t)^2 t p_1 + 3(1-t)t^2 p_2 + t^3 p_3 \end{pmatrix} &= \begin{pmatrix} 1 & 0 & 0 & 0 \\ (1-t) & t & 0 & 0 \\ (1-t)^2 & 2(1-t)t & t^2 & 0 \\ (1-t)^3 & 3(1-t)^2 t & 3(1-t)t^2 & t^3 \end{pmatrix} \begin{pmatrix} p_0 \\ p_1 \\ p_2 \\ p_3 \end{pmatrix} \\ & \\ H_1 &= \begin{pmatrix} (1-t)^3 p_0 + 3(1-t)^2 t p_1 + 3(1-t)t^2 p_2 + t^3 p_3 \\ (1-t)^2 p_1 + 2(1-t)t p_2 + t^2 p_3 \\ (1-t) p_2 + t p_3 \\ p_3 \end{pmatrix} &= \begin{pmatrix} (1-t)^3 & 3(1-t)^2 t & 3(1-t)t^2 & t^3 \\ 0 & (1-t)^2 & 2(1-t)t & t^2 \\ 0 & 0 & (1-t) & t \\ 0 & 0 & 0 & 1 \end{pmatrix} \begin{pmatrix} p_0 \\ p_1 \\ p_2 \\ p_3 \end{pmatrix}\end{split}\]

从中可以定义一个 \((8, 4)\) 分割矩阵 \(S_3\)，它可以乘以 points 数组以计算返回值

\[\begin{split}S_3 &= \begin{pmatrix} 1 & 0 & 0 & 0 \\ (1-t) & t & 0 & 0 \\ (1-t)^2 & 2(1-t)t & t^2 & 0 \\ (1-t)^3 & 3(1-t)^2 t & 3(1-t)t^2 & t^3 \\ (1-t)^3 & 3(1-t)^2 t & 3(1-t)t^2 & t^3 \\ 0 & (1-t)^2 & 2(1-t)t & t^2 \\ 0 & 0 & (1-t) & t \\ 0 & 0 & 0 & 1 \end{pmatrix} \\ & \\ S_3 P &= \begin{pmatrix} 1 & 0 & 0 & 0 \\ (1-t) & t & 0 & 0 \\ (1-t)^2 & 2(1-t)t & t^2 & 0 \\ (1-t)^3 & 3(1-t)^2 t & 3(1-t)t^2 & t^3 \\ (1-t)^3 & 3(1-t)^2 t & 3(1-t)t^2 & t^3 \\ 0 & (1-t)^2 & 2(1-t)t & t^2 \\ 0 & 0 & (1-t) & t \\ 0 & 0 & 0 & 1 \end{pmatrix} \begin{pmatrix} p_0 \\ p_1 \\ p_2 \\ p_3 \end{pmatrix} = \begin{pmatrix} \vert \\ H_0 \\ \vert \\ \vert \\ H_1 \\ \vert \end{pmatrix}\end{split}\]

参数:

• points (BezierPointsLike) – 贝塞尔曲线的控制点。

• t (float) – 用于分割贝塞尔曲线的 t 值。

返回:

一个包含定义两条贝塞尔曲线的控制点的数组。

返回类型:

Point3D_Array

subdivide_bezier(points, n_divisions)

将贝塞尔曲线细分为 \(n\) 条形状相同的子曲线。

曲线被分割的点位于参数 \(t = \frac{i}{n}\) 处，其中 \(i \in \{1, ..., n-1\}\)。

另请参阅

• 有关如何分割贝塞尔曲线的解释，请参见 split_bezier()。

• 有关此函数的更多理解，请参见 partial_bezier_points()。

注意

所得子曲线可以表示为 points 的线性组合，这些组合可以编码在一个矩阵中，该矩阵已为二次和三次贝塞尔曲线预先计算。

以二次贝塞尔曲线为例：借鉴 partial_bezier_points() 中的解释，其中定义了以下矩阵 \(P_2\) 以提取二次贝塞尔曲线在 \(t \in [a, b]\) 范围内的部分

\[\begin{split}P_2 = \begin{pmatrix} (1-a)^2 & 2(1-a)a & a^2 \\ (1-a)(1-b) & a(1-b) + (1-a)b & ab \\ (1-b)^2 & 2(1-b)b & b^2 \end{pmatrix}\end{split}\]

计划是将 \([a, b]\) 替换为 \(\left[ \frac{i-1}{n}, \frac{i}{n} \right], \ \forall i \in \{1, ..., n\}\)。

以 \(n = 2\) 细分为例，构造区间 \(\left[ 0, \frac{1}{2} \right]\) 的 \(P_1\)，以及区间 \(\left[ \frac{1}{2}, 1 \right]\) 的 \(P_2\)

\[\begin{split}P_1 = \begin{pmatrix} 1 & 0 & 0 \\ 0.5 & 0.5 & 0 \\ 0.25 & 0.5 & 0.25 \end{pmatrix} , \quad P_2 = \begin{pmatrix} 0.25 & 0.5 & 0.25 \\ 0 & 0.5 & 0.5 \\ 0 & 0 & 1 \end{pmatrix}\end{split}\]

因此，可以构造以下 \((6, 3)\) 细分矩阵 \(D_2\)，它将把 points 数组细分为 2 部分

\[\begin{split}D_2 = \begin{pmatrix} M_1 \\ M_2 \end{pmatrix} = \begin{pmatrix} 1 & 0 & 0 \\ 0.5 & 0.5 & 0 \\ 0.25 & 0.5 & 0.25 \\ 0.25 & 0.5 & 0.25 \\ 0 & 0.5 & 0.5 \\ 0 & 0 & 1 \end{pmatrix}\end{split}\]

对于二次和三次贝塞尔曲线，细分矩阵会进行记忆化以提高效率。对于更高次的曲线，则改用受 split_bezier() 启发而来的迭代算法。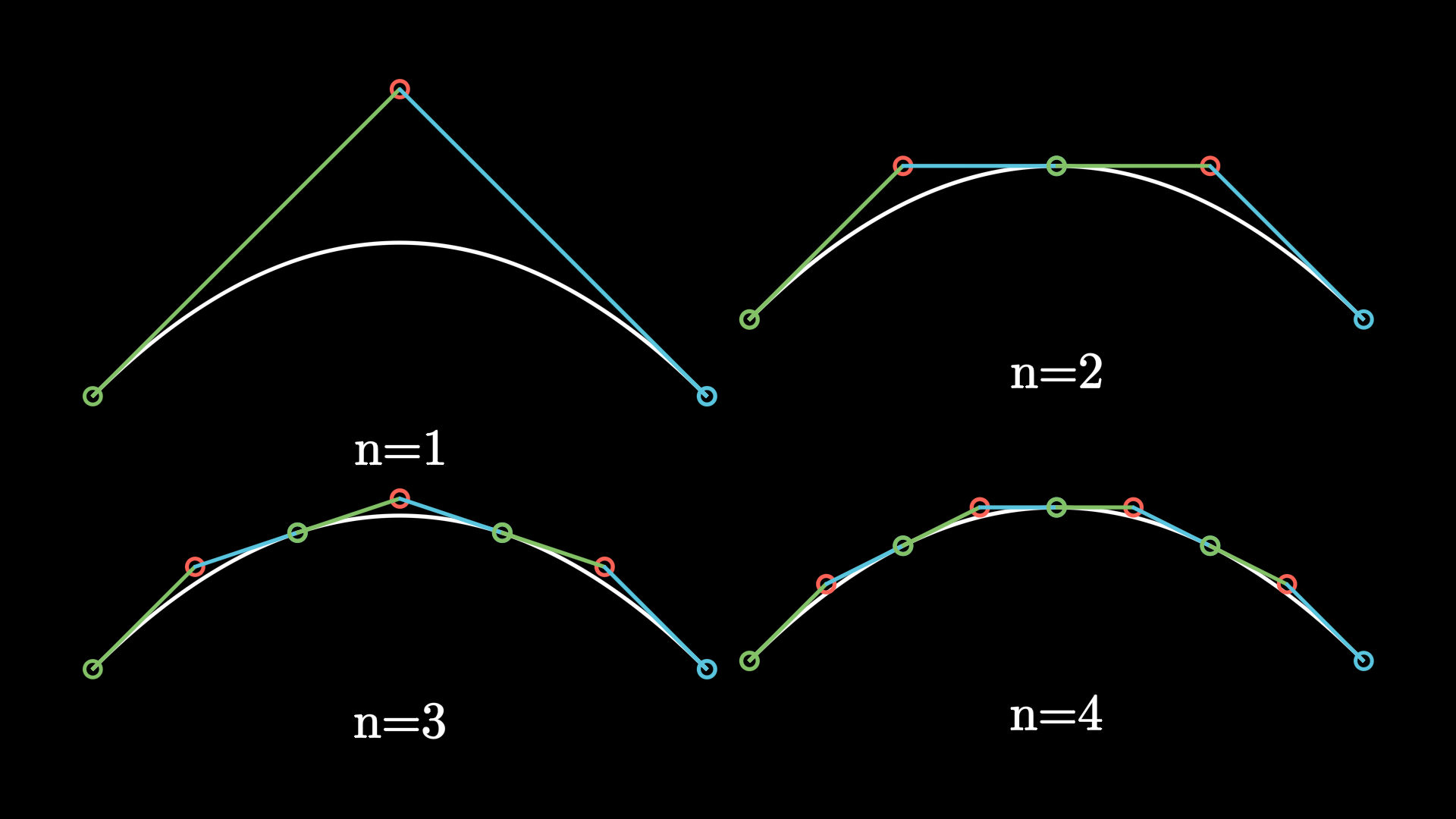

参数:

• points (BezierPointsLike) – 贝塞尔曲线的控制点。

• n_divisions (int) – 将贝塞尔曲线细分为的曲线数量

返回:

一个包含定义新 \(n\) 条子曲线的点的数组。

返回类型:

样条